Volume-Filtered Immersed Boundary method

The Immersed Boundary Method (IBM) is a fully resolved approach towards multiphase flows originally proposed by Peskin (Flow patterns around heart valves: A numerical method in Journal of Computational Physics, 1972) to study blood flow around heart valves. Later, Uhlmann (An immersed boundary method with direct forcing for the simulation of particulate flows in Journal of Computational physics, 2005) presented a notable improvement over Peskins approach forcing the immersed boundary using a cloud of Lagrangian markers that define the surface of the solid. The forcing between the fluid Eulerian points and the solid surface Lagrangian points is coupled using interpolation and spreading techniques using the regularized Dirac delta. Many recent advances are based on Uhlmanns approach of the IBM formulation and show great improvement in the accuracy of the quantities calculated at the interface.
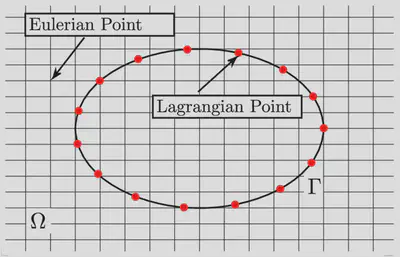
This approach has recently gained significant traction with the increase in computational power recently due to its many benefits over conventional multiphase simulation approaches such as the body-fitted method. One of its most attractive features is the ability to allow for moving interfaces without the need for mesh regeneration, providing an significant increase in computational efficiency by saving time per step.
While recent advances show significant improvement, certain questions still remain unanswered which stem from the ad-hocness of the methods:
- What is the role of the internal flow within the immersed solid and how does it affect the quantities calculated at the interface?
- What is the correct way to compute the Lagrangian marker volumes which arise during the computation of the forcing at the markers?
- What is the accurate way to compute the hydrodynamic force at the interface?
We propose to answer these questions and attempt to properly formalize the forcing at the interface using the concept of volume filtering proposed by Anderson and Jackson (Fluid Mechanical Description of Fluidized Beds. Equations of Motion in Industrial & Engineering Chemistry Fundamentals, 1967). This approach is similar in fashion to the Large-Eddy Simulation (LES) approach. The Navier-Stokes Equations are filtered with a filter kernal having a compact width of $\delta_f$. This produces the filtered Navier-Stokes Equations where the boundary conditions appear as right-hand-side terms involving surface integrals on the immersed boundary. Furthremore, sub-filter-scale terms arise similar in spirit to the LES equations which can be modeled, providing a path towards LES for immersed boundaries.
The new Volume Filtered Immersed Boundary (VFIB) method is tested against various moving and static boundaries and shows excellent accuracy compared to previous IBM formulations, body-fitted approaches and experimental results.
Some examples of simulations using the VFIB approach
- Laterally oscillating cylinder with cross flow at $Re_D = 185$: isocontours of positive (orange) and negative (green) vorticity are presented to show the wake behind the cylinder.
- Simulation of rotating blades on a drone to show the ability of the VFIB model to accomodate complex geometries: vorticity is displayed showing vortex structures in the wake of the blade.
Related Publications
- Dave, H., Herrmann, M. & Kasbaoui, M. H., The volume-filtering immersed boundary method, Journal of Computational Physics, 487, 112136 (08/15/2023).
- Dave, H., Herrmann, M., Brady, P., & Kasbaoui, M.H., Characterization of the forcing and sub-filter scale terms in the volume-filtering immersed boundary method, Journal of Computational Physics, 525, 113765 (03/15/2025)